A quart de primària el currículum ens demana que treballem la suma i resta de nombres de quatre dígits i més. Abans de llençar-nos-hi de ple, vam dedicar dues sessions a compilar totes les estratègies preferides pels alumnes: primer per a la suma i després per a la resta. Us podeu imaginar que s’ho van prendre com un repte! Quantes maneres diferents serien capaços de trobar?
Vam començar donant un sol problema a tota la classe. Només els vam dir que havien de resoldre el problema de tantes formes diferents com els fos possible. Com sempre, vam posar al seu abast tot el material manipulable que tenim i els vam encoratjar a fer-lo servir: regletes de base 10, fitxes de dos colors, discos de valor posicional i rajoles d’àrea.
Primer vam donar-los un temps per treballar sols per a que cadascú pogués pensar. Al cap d’uns deu minuts els vam demanar que treballesin amb la seva parella matemàtica per compartir idees i també per intentar trobar noves estratègies. Finalment vam demanar que sortissin voluntaris a explicar a tota la classe com havien solucionat el problema. Aquest moment de posada en comú és molt potent, ja que el mestre se situa en un segon pla i són els alumnes qui porten tot el discurs matemàtic, fent-se preguntes i esclarint dubtes entre ells. Segons Danielson (2007), aquest seria un exemple de la màxima eficiència docent.
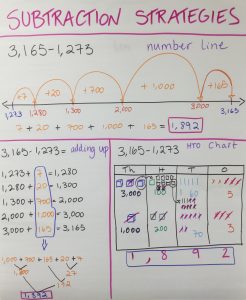
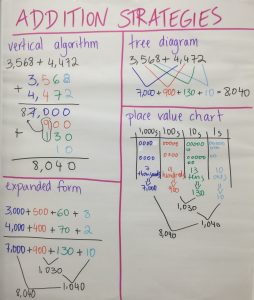
Tot i que intentàvem no repetir idees, al cap d’una estona vam veure que algunes de les estratègies eren molt similars i vam decidir ajuntar-les o reestructurar-les. Com podeu veure a les fotos, va sortir molta descomposició, cosa que ens fa molt contents, ja que demostra que els nostres alumnes tenen molta flexibilitat numèrica. Hi va haver algun intent de fer servir l’algorisme tradicional, però els alumnes no van saber explicar per què o com funcionava i al final el vam descartar.
L’endemà vam fer el mateix procés amb la resta i el resultat també va ser molt positiu.
Aquest va ser un punt de partida molt sòlid per a començar a treballar operacions amb nombres més grans. Els pósters que vam fer continuen penjats a la classe com a referència.
Aviat farem el mateix amb la multiplicació i la divisió. Ja ho compartirem amb tots vosaltres!